H-TSP[2023]: Hierarchically TSP Using RL Transformer

https://www.microsoft.com/en-us/research/uploads/prod/2023/02/8643.PanX_.pdf

The author of this paper is from Huazhong University of Science and Technology, China, University of Science and Technology of China, and Microsoft Research Asia. Their work is publish in the AAAI 2023.

They are dealing with the ML algorithm scalabilty problem in TSP. Most ML model hard to scale to large scale problem. Although the work of Prof Zha’s Att+GCN+MCTS can scale to large problem, the Monte Carlo tree search procedure is required to improve solutions onstantly, which is still time-consuming. (See my blog about this paper)

Att-GCN+MCTS [2021] Generalize a Small Pre-trained Model to Arbitrarily Large TSP Instances

Acknowledgments go to Prof. Zha and his dedicated students. This paper, a product of research conducted at my alma mater, The Chinese University of Hong Kong, Shenzhen, found its place in the prestigious 2021 AAAI publication.

https://58191554.github.io/paperRead/Att-GCN+MCTS[2021].html

This paper’s target is solving the problem that when action spaces grow linearly in the number of cities, their training procedures would easily run out of memory or time before converging to some near-optimal solutions. They choose a small subset of graph, solve it in a open loop TSP, and merge them sub-TSP path to the existing partial route. Iteratively do this untill all the cities are involved in the route.

The Hierarchical Framework

Looking at the high level idea, it is a straight idea, use the upper level network to generate the subproblem while not finished, solve the subproblem with the lower level network, and then merge the sub-solution to the whole solution.

A different thing from the algorithm of Att+GCN+MCTS, they gradual solve the sub-problem, and merge step by step, instead of generating all the sub-solution all together. In this paper, they said that by interleaving decomposition and merging, the upper-level model can learn an adaptive
policy that can make its best decision based on current partial solution and distribution of remaining nodes

A Scalable Encoder

They took the idea of 3D point could, and build a encoder for a large scale graph. They put a grid to the graph, and augment features of each node with a vector , the absolute coordinate of the node, the relative coordinates to the gird center and the node cluster center, respectively.

For a TSP instance with N nodes, we have a tensor of size (N, D), where D = 11 is the number of features. The feature is the output of the permutative-invariant network. Then this tensor is processed by a linear layer to generate a (N, C) sized high dimensional tensor.

The DRL model follows the actor-critic architecture (PPO). Train the PPO with this minimizing this objective function:

L(\theta) = \hat{\mathbb{E}}_t[\min(r_t(\theta)\hat{A}_t, clip(r_t(\theta), 1-\epsilon, 1+\epsilon)\hat{A}_t)]

r_t(\theta) = \frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}

$r_t(\theta)$ denotes the probability ratio of two policies. The advantage function represents the advantage of the current policy over the old policy

\hat{A}_t = \sum_{l = 1}^\infty (\gamma \lambda)^l(r_t+\gamma\hat{V}(s_{t+l+1})-\hat{V}(s_{t+l}))

Here $r_t$ is the reward, and $λ$ is the hyper-parameter that controls the compromise between bias and variance of the estimated advantage. Besides the policy loss, we also add the value loss and
entropy loss:

L^{\hat{V}}(\theta) = \hat{\mathbb{E}}_t[\hat{V}-\hat{V}_\theta]^2

L^E(\theta) = \hat{\mathbb{E}}_t[\pi_\theta(a|s)\log(\pi_\theta(a|s))]

Sub-Problem Generation and Merging

After the Scalable Encoder encode the graph into vertexs with features, they use Actor-Critic to choose the next vertex $v_b$ . Using kNN we find a cluster of sub problem, and solve the sub-problem with a Encoder-Decoder Transformer. Because the local open TSP solution is with two ends, which is not symetric. They use a trick: During the node selection, all nodes except the endpoints will be treated as in TSP without any constraint. Whenever an endpoint is chosen, we let the other one be chosen automatically. The final solution of the origin open-loop TSP is obtained by removing the redundant edge between the two endpoints.

The lower-level use the classic REINFORCE

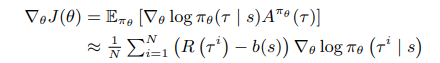
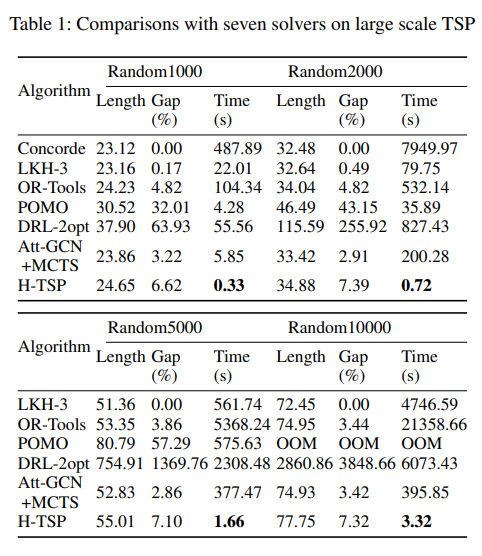
Experiment

Although the result of the H-TSP is not the shortest compared to Att-GCN+MCTS, but is is very fast, especially when the graph is big over 1000. In the 5000 city TSP,